Nota: No tengo mucho conocimiento sobre series temporales; esta idea surgió mientras leía un libro de estadística. Este miniartículo no tiene un rigor matemático profundo, pero está diseñado para ser ameno y accesible.

En este microartículo, vamos a generar una serie temporal aleatoria utilizando distribuciones de probabilidad continuas. Un dato importante a tener en cuenta es que las computadoras, por su naturaleza determinista, no pueden generar números completamente aleatorios. Dado que para una entrada específica siempre producirán la misma salida, lo que realmente generan son números pseudoaleatorios, aprovechando distintos métodos y algoritmos. Sin embargo, no profundizaremos en cómo funcionan estos generadores, ya que el objetivo de este artículo es otro.

Para ello, utilizaremos una librería de Python que permite generar números aleatorios siguiendo distribuciones de probabilidad como la normal, beta o gamma, entre otras.

Supongamos que el precio de una acción varía a lo largo del día. Al abrir el mercado, se registra el precio de apertura, y al cerrarlo, el precio de cierre, que no necesariamente es el mismo. Puede ser mayor o menor. Una forma sencilla de cuantificar este cambio es mediante la siguiente fórmula:

$$ p = \frac{p_f}{p_0} $$

donde:

• p_0 es el precio de apertura.
• p_f es el precio de cierre.

Si ( p = 1 ), significa que la acción mantuvo su valor. Si ( p > 1 ), la acción aumentó de precio, y si ( p < 1 ), el precio cayó. Este valor, nombrado como factor de crecimiento, nos da una idea de cómo evoluciona el precio de la acción a lo largo del tiempo.

Introducción de la aleatoriedad

El factor de crecimiento P no es un valor fijo, sino una variable aleatoria continua, lo que significa que puede tomar distintos valores dentro de un rango. Su comportamiento puede modelarse mediante una distribución de probabilidad, como la distribución normal, cuya función de densidad de probabilidad está dada por:

$$ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}} $$

donde:

• μ es la media de la distribución.
• σes la desviación estándar.

La idea es ajustar estos parámetros para que la distribución se adapte a nuestras necesidades. En este caso, necesitamos generar números aleatorios alrededor de 1, con una desviación estándar pequeña. A primera vista, esto podría parecer una suposición arbitraria, pero tiene sentido si lo analizamos bien: en un solo día, el precio de una acción suele variar poco. Aunque cambios bruscos no son imposibles, son poco probables. Teniendo esto en cuenta, es lógico que la media de nuestra distribución sea 1 (o cercana a 1), y que la desviación estándar sea un número pequeño y positivo. Para verificar esta hipótesis, podemos calcular el factor de crecimiento de acciones reales. En este caso, tomaremos los datos de Apple (AAPL) desde 2021 hasta 2024 y generaremos un histograma a partir de ellos.

Nota: No necesariamente esto se cumple para todas las acciones.

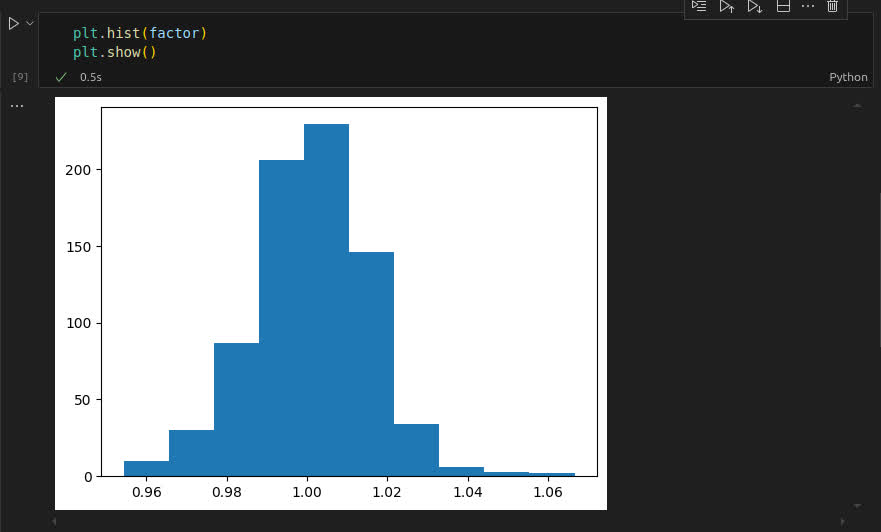
Como se observa en la imagen, la distribución del factor de crecimiento de Apple tiene una forma similar a la distribución normal. Con esta base, procederemos a generar nuestra serie temporal aleatoria.

A lo nuestro. Lo único que debemos hacer es generar números aleatorios siguiendo una distribución normal, con un valor de μ igual a 1 (o muy cercano) y una σ pequeña. Para determinar un valor adecuado de σ, podemos basarnos en la desviación estándar del conjunto de datos de la acción de Apple o realizar pruebas hasta encontrar un valor que se ajuste correctamente.

Implementé todo lo anterior en el siguiente código de Python:

start_value = 10
random_factor = np.random.normal(1, 0.1, 100)

values = []
for index, factor in enumerate(random_factor):
    start_value = start_value * factor
    values.append([index, start_value])
values = np.array(values).T

plt.plot(values[0], values[1])
plt.show()

Aquí algunos ejemplos de series temporales. Si observamos con atención, esta forma de generarlas tiene ciertas limitaciones. Si el valor de σ es demasiado alto, la serie se vuelve altamente volátil y poco realista. En la mayoría de los casos, las series temporales siguen una tendencia o presentan comportamientos cíclicos, aspectos que este método no captura completamente.

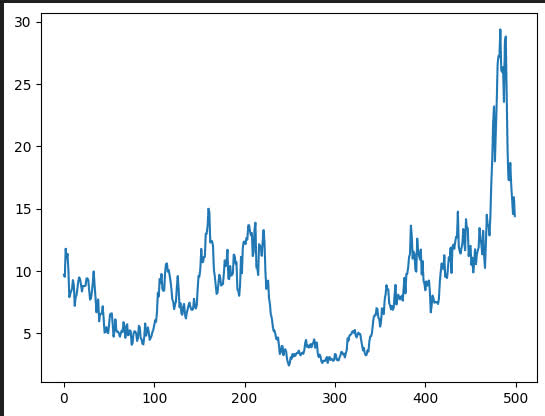
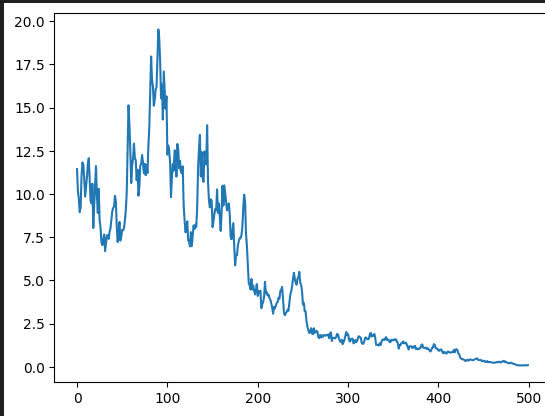
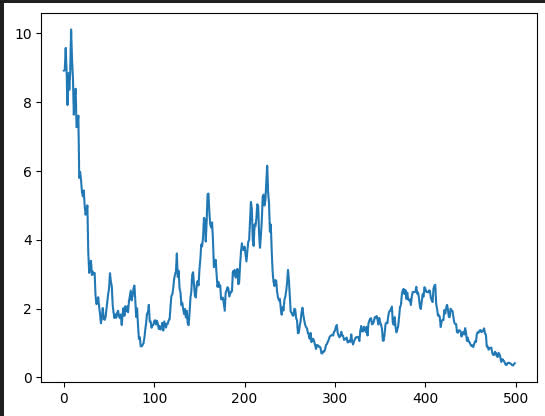
Ahora vamos a experimentar con esto, pero antes, veamos la fórmula recursiva para nuestras series. Podemos hacer varias modificaciones, como probar con diferentes distribuciones o agregar más términos a la fórmula original.

$$ v_{n+1} = v_n \cdot f_{random} $$

Vamos a explorar otra distribución, la distribución gamma, que es fundamental conocer debido a su relevancia en estadística. Es una distribución muy interesante, tanto por la función gamma en sí misma como por su presencia en diversos aspectos de la estadística. La función de densidad de probabilidad de la distribución gamma es cero para cualquier número menor que cero, y sus parámetros deben ser mayores que cero. La expresión de la función de densidad de probabilidad es la siguiente:

$$ f(x) = \frac{1}{\Gamma(\alpha) \theta^\alpha} x^{\alpha - 1} e^{-\frac{x}{\theta}} $$

A diferencia de la distribución normal, no existe una forma sencilla de elegir los parámetros correctos de manera intuitiva. Como creo que los números explican mejor que las palabras, continuaré deduciendo los parámetros adecuados para esta distribución. Comencemos calculando el (n)-ésimo momento central de una variable aleatoria.

$$ \mu_r = E[X^r] = \int_{-\infty}^{+\infty} x^r f(x)dx. $$

Nota: No utilizaré el límite, aunque debería ser considerado en un análisis más riguroso.

Sustituyendo la función de densidad de probabilidad de la distribución gamma, tenemos:

$$ \mu_r = \frac{1}{\Gamma(\alpha) \theta^\alpha} \int_{0}^{+\infty} x^r x^{\alpha - 1} e^{-\frac{x}{\theta}} dx $$

Realizamos un cambio de variable y simplificamos la expresión:

$$ u = \frac{x}{\theta}, \quad \theta du = dx $$

Sustituyendo en la integral, obtenemos:

$$ \mu_r = \frac{1}{\Gamma(\alpha) \theta^\alpha} \int_{0}^{+\infty} (\theta u)^{\alpha + r - 1} e^{-u} \theta du $$

Simplificando:

$$ \mu_r = \frac{1}{\Gamma(\alpha) \theta^\alpha} \theta^{\alpha + r} \int_{0}^{+\infty} u^{\alpha + r - 1} e^{-u} \theta du $$

$$ \mu_r = \frac{1}{\Gamma(\alpha)} \theta^r \Gamma(\alpha + r) $$

Finalmente, el (r)-ésimo momento central es:

$$ \mu_r = \theta^r \frac{\Gamma(\alpha + r)}{\Gamma(\alpha)} $$

Con esta fórmula, podemos calcular la media y la desviación estándar. El primer momento central es igual a la media, es decir:

$$ \mu = \theta^1 \frac{\Gamma(\alpha + 1)}{\Gamma(\alpha)} = \theta \frac{\alpha \Gamma(\alpha)}{\Gamma(\alpha)} = \theta \alpha $$

Para calcular la desviación estándar, utilizamos la varianza, que es el segundo momento alrededor de la media al cuadrado:

$$ \sigma^2 = E[(X - \mu)^2]. $$

Desarrollamos la expresión:

$$ \sigma^2 = E[X^2 - 2\mu X + \mu^2] = E[X^2] - 2\mu E[X] + \mu^2 E[1] $$

$$ \sigma^2 = E[X^2] - 2\mu^2 + \mu^2 $$

$$ \sigma^2 = E[X^2] - \mu^2 $$

Por lo tanto, la desviación estándar es:

$$ \sigma = \sqrt{E[X^2] - \mu^2} $$

Sustituyendo en la fórmula, obtenemos:

$$ \sigma = \sqrt{\theta^2 \alpha (\alpha + 1) \frac{\Gamma(\alpha)}{\Gamma(\alpha)} - (\theta \alpha)^2} $$

Simplificando:

$$ \sigma = \sqrt{\theta^2 \alpha (\alpha + 1) - \theta^2 \alpha^2} $$

$$ \sigma = \sqrt{\theta^2 \alpha} $$

Finalmente, obtenemos la desviación estándar:

$$ \sigma = \theta \sqrt{\alpha} $$

Con estas dos expresiones, podemos ajustar los valores de los parámetros según nuestras necesidades:

$$ \mu = \theta \alpha $$

$$ \sigma = \theta \sqrt{\alpha} $$

continuar aqui y piensa en como generar

---

Sin embargo, vamos a ir un paso más allá. ¿Les suenan las distribuciones bivariadas? En lugar de usar un solo factor de crecimiento, podemos introducir otros parámetros que sigan una aleatoriedad no uniforme, enriqueciendo así el comportamiento de la serie.

En este punto, he omitido muchas teoría fascinante sobre estadística. Si les interesa profundizar, les recomiendo Canavos, un libro muy completo (aunque extenso). Sin embargo, siempre me han gustado los gráficos, y esta es una excelente oportunidad para explicar visualmente algunos conceptos antes de experimentar. Así que, antes de jugar un poco, veamos qué son y cómo funcionan las distribuciones bivariadas.